
The time complexity to locate the top priority element is constant. The binary search tree becomes a priority queue if the sort order is based on priority. To maintain items efficiently in sorted order, a binary search tree is utilised.

However, to do the delete and peek operation, you must traverse the array and hence, the worst-case time complexity is O(n) for both. Hence to insert an element, it does not matter where you insert it and hence it takes O(1) time. In an unordered array, all the elements are not arranged according to priority. Since they are in order, both the delete and the peek operations take O(1) time. To insert a new element, you must traverse the array and insert it in such a way that the ordering is maintained.
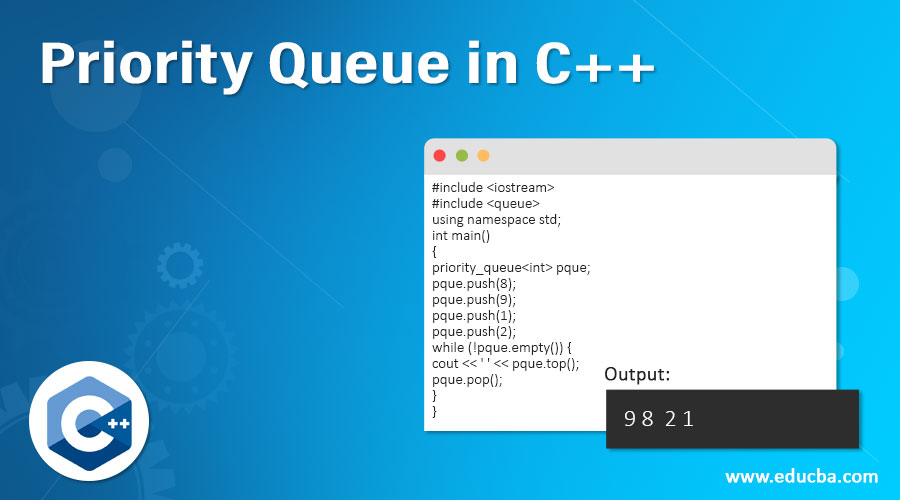
In an ordered array, all the elements are ordered according to priority. The first is to use an ordered array and the other is to use an unordered array. There are two ways to go about implementation of priority queues using arrays. For insertion and deletion, the heapify operation must be done and hence the time complexity for the same is O(log n) each. Insertion and Deletion operations using Heap are illustrated in the next section. The top priority element is present at the root node of the heap and hence the peek operation has a time complexity of O(1). This is the most efficient implementation of a Priority Queue. Since the highest priority element is present at the head of the list, it takes just O(1) time to remove it or to do the peek() operation. Peek() is used to retrieve the highest priority element without removing it and this is also present at the head of the list. the element that entered the priority queue first will be the first to be removed.įor deletion, the highest priority element will be removed first from the priority queue and the highest priority element is at the head of the list and hence it will simply be removed. If two elements in the queue have the same priority value then the first in first out rule is followed for these two elements alone i.e.Higher or lower priority elements must be dequeued before lower or higher priority elements respectively depending on priority order taken by user that is if user consider lower number as higher priority or higher number as higher priority.Each item in the queue must have a priority associated with it.Characteristics of a Priority QueueĪ queue is called a Priority Queue when it has the following characteristics: (in such a way that the highest priority elements are moved to the beginning of the queue and the lowest priority elements are moved to the back of the queue). Hence, the items in the priority queue are arranged in either ascending or descending order depending on the priority value taken by the user. However, in a Priority Queue, each item in the queue is assigned a priority, and items are dequeued or removed based on this priority value assigned to them.
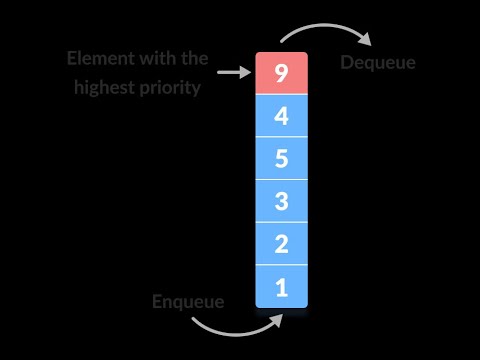
Just like any queue we form, the person that stands first in the queue, will be addressed first and similarly, even in computer science queues, the same rule applies. In a normal Queue, first-in-first-out is followed which means that whichever elements enters the queue first, will be the first to leave. It is an Abstract Data Type that functions a little differently than a normal Queue. if the two elements are a and b, they should follow one of the conditions:Īs a result, the items in the priority queue are arranged in ascending or descending order. Elements are called comparable if they are either lesser than, equal to or greater than one another, i.e. It is important to note that a priority queue only supports elements that are comparable.


 0 kommentar(er)
0 kommentar(er)
